## Mesures de réseaux d'interaction
### 2-Quelques mesures de base:
| Mesure | Resultat|
|-----------------|:-------------|
| Le nombre de noeud (N) :| 317080 |
| Le nombre de lien (L) : | 1049866 |
| Le Degré moyen (K) :| 6.62208890914917 |
| Le coefficient de clustering : | 0.6324308280637396 |
Le coefficient de clustering pour un réseau aléatoire de la même taille et du même degré moyen est : ****
----
### 3-La connexité du reseau
Oui, le reseau est connexe car il posséde une seule composante connexe (il suffit d'executer ce code)
```java
if(isConnected(graph))
System.out.println("Le graphe est connexe");
else
System.out.println("Le graphe est non connexe");
```
Un réseau aléatoire de la même taille et degré moyen ne sera pas connexe car dans un régime connecté cette condition doit etre verifiée :
 (p > \frac{ln(N)}{N})) et là dans notre cas :
et là dans notre cas :
 = 12.666909387 ) Donc un réseau aléatoire avec cette taille sera connexe à partir d'un degré
moyen superieur à
Donc un réseau aléatoire avec cette taille sera connexe à partir d'un degré
moyen superieur à  ----
### 4-La distribution des degrés
Il faut créer un fichier contenant les degrés et leurs distributions, en executant
avec gnuplot on aura ces 2 resultats:
En traçant la distribution de degrés en échelle log-log on observe une ligne droite
pendant plusieurs ordres de grandeur. Cela nous indique une loi de puissance :
----
### 4-La distribution des degrés
Il faut créer un fichier contenant les degrés et leurs distributions, en executant
avec gnuplot on aura ces 2 resultats:
En traçant la distribution de degrés en échelle log-log on observe une ligne droite
pendant plusieurs ordres de grandeur. Cela nous indique une loi de puissance :
 Tracer la distribution et estimer l'exposant de la loi de puissance:
Tracer la distribution et estimer l'exposant de la loi de puissance:
| tracer la distribution des degrés | |
:--------------------------:|:-------------------------:
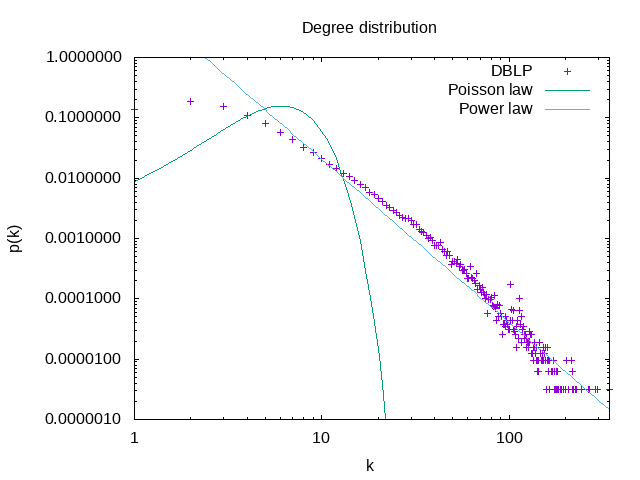 |
On a γ=2.7±0.04
La loi de puissance ici signifie que ce reseau n'a pas d'échelle, comme
on a pu le remarquer lors du calcul de la distribution le degré typique
des noeuds est k ± ∞.
----
### 5-La distance moyenne dans le réseau
Voici le programme utilisé:
```java
public static HashMap getDistancesDistribution(Graph g, int nn) {
List sample = Toolkit.randomNodeSet(g, nn);
HashMap dist_distances = new HashMap<>();
int i = 0;
for (Node n : sample) {
BreadthFirstIterator iter = (BreadthFirstIterator) n.getBreadthFirstIterator();
while (iter.hasNext()) {
int depth = iter.getDepthOf(iter.next());
Double depthSum = dist_distances.get(depth);
if (depthSum == null)
dist_distances.put(depth, 1.0);
else
dist_distances.put(depth, depthSum + 1);
}
i++;
System.out.format("\r%.1f%% complété", ((double) i) / 1000 * 100);
}
Double measuresCount = dist_distances.values().stream().reduce(0.0, Double::sum);
dist_distances.forEach((k, v) -> dist_distances.put(k, v / measuresCount));
return dist_distances;
}
```
La courbe obtenue :
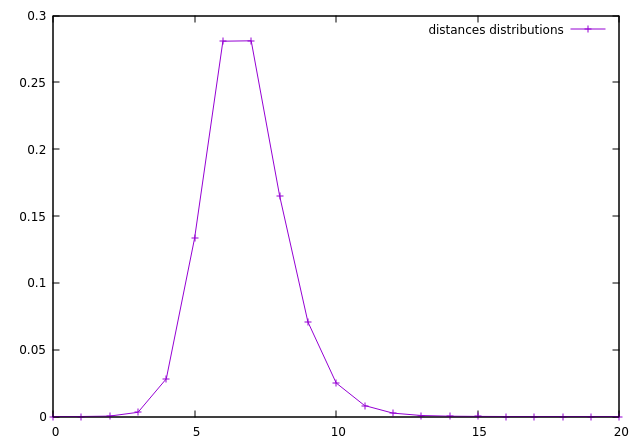
La distance moyenne obtenue avec un échantillon de 1000 est :6;76 par consequant
L'hypothèse des 6 degrés de séparation semble se confirmer.
Pour savoir s'il s'agit d'un réseau "petit monde", il suffit de vérifier que d=d(max)
}{ln(K)}=6.71) et vue que
d et d(max) ne sont pas égaux mais notre algorithme ne permet pas d'avoir un résultat d'une immense précision,
on pourra en conclure que le réseau de collaboration est un petit monde.
......................
### 6-Refaire les mesures de base
En utilisant GraphStream, on génere un réseau aléatoire et un
un réseau avec la méthode d'attachement préférentiel (Barabasi-Albert)
(même taille et même degré), et on refait les mesures précédentes :
1)Un réseau avec la méthode d'attachement préférentiel (Barabasi-Albert) :
| Mesure | Resultat|
|-----------------|:-------------|
| Le nombre de noeud (N) :| 100000 |
| Le nombre de lien (L) : | 349539 |
| Le Degré moyen (K) :| 6.990779876708984 |
| Le coefficient de clustering : | 0.0012226869597521156 |
Oui, ce graphe est connexe.
| tracer la distribution des degres et estimer l'exposant de la loi de puissance | |
:--------------------------:|:-------------------------:
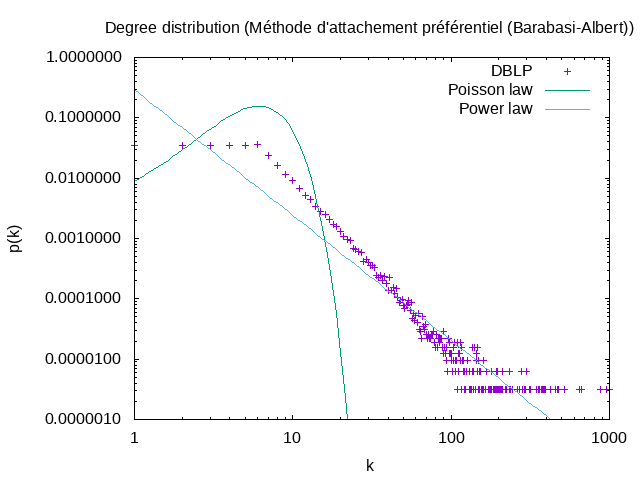 |
| tracer la distribution des distances | |
:--------------------------:|:-------------------------:
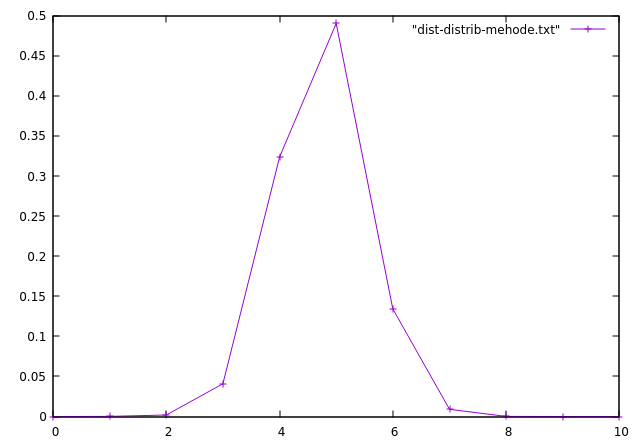 |
2)Un réseau aléatoire :
| Mesure | Resultat|
|-----------------|:-------------|
| Le nombre de noeud (N) :| 100000 |
| Le nombre de lien (L) : | 348924 |
| Le Degré moyen (K) :| 6.978549957275391 |
| Le coefficient de clustering : | 6.77163144670172E-5 |
Ce réseau n'est pas connecté.
| tracer la distribution et estimer l'exposant de la loi de puissance | |
:--------------------------:|:-------------------------:
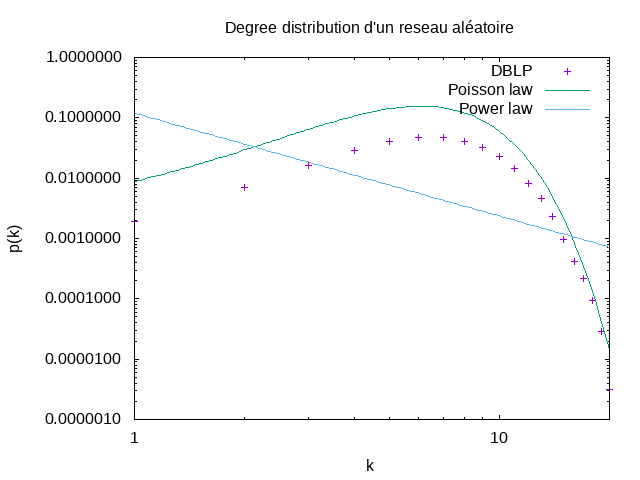 |
| tracer la distribution des distances | |
:--------------------------:|:-------------------------:
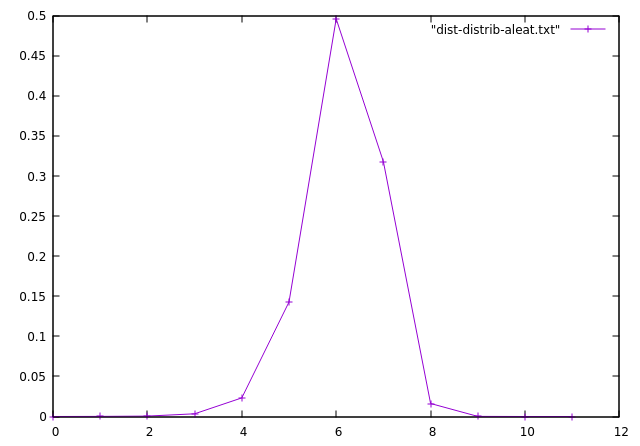 |
et vue que
d et d(max) ne sont pas égaux mais notre algorithme ne permet pas d'avoir un résultat d'une immense précision,
on pourra en conclure que le réseau de collaboration est un petit monde.
......................
### 6-Refaire les mesures de base
En utilisant GraphStream, on génere un réseau aléatoire et un
un réseau avec la méthode d'attachement préférentiel (Barabasi-Albert)
(même taille et même degré), et on refait les mesures précédentes :
1)Un réseau avec la méthode d'attachement préférentiel (Barabasi-Albert) :
| Mesure | Resultat|
|-----------------|:-------------|
| Le nombre de noeud (N) :| 100000 |
| Le nombre de lien (L) : | 349539 |
| Le Degré moyen (K) :| 6.990779876708984 |
| Le coefficient de clustering : | 0.0012226869597521156 |
Oui, ce graphe est connexe.
| tracer la distribution des degres et estimer l'exposant de la loi de puissance | |
:--------------------------:|:-------------------------:
 |
| tracer la distribution des distances | |
:--------------------------:|:-------------------------:
 |
2)Un réseau aléatoire :
| Mesure | Resultat|
|-----------------|:-------------|
| Le nombre de noeud (N) :| 100000 |
| Le nombre de lien (L) : | 348924 |
| Le Degré moyen (K) :| 6.978549957275391 |
| Le coefficient de clustering : | 6.77163144670172E-5 |
Ce réseau n'est pas connecté.
| tracer la distribution et estimer l'exposant de la loi de puissance | |
:--------------------------:|:-------------------------:
 |
| tracer la distribution des distances | |
:--------------------------:|:-------------------------:
 |