# Mesures de réseaux d'interaction
### 2-Quelques mesures de base:<br />
Le nombre de noeud (N) =  317080<br />
Le nombre de lien (L) =  1049866<br />
Le Degré moyen (K) =  6.62208890914917<br />
Le coefficient de clustering = : 0.6324308280637396<br />
-Le coefficient de clustering pour un réseau aléatoire de la même taille et du même degré moyen :<br />
<img src="https://latex.codecogs.com/svg.latex?\Large&space;P=\frac{K}{N}=\frac{6.62208890914917}{317080}=0.00002088459" />
----
### 3-La connexité du reseau
-Oui, le reseau est connexe car il posséde une seule composante connexe (il suffit d'executer ce code)
```java
ConnectedComponents connexe = new ConnectedComponents();
            connexe.init(graph);
            if(connexe.getConnectedComponentsCount()==1){
                System.out.println("le graphe est connexe");
             }       
```
-Un réseau aléatoire de la même taille et degré moyen ne sera pas connexe car dans un régime connecté cette condition doit etre verifiée : <br />
<img src="https://latex.codecogs.com/svg.latex?\Large&space;k >ln(n) (p > \frac{ln(N)}{N})" title="" /><br /><br />
 et là dans notre cas :&nbsp;
<img src="https://latex.codecogs.com/svg.latex?\Large&space;k = 6.62208890914917  "/>&nbsp; et &nbsp;
<img src="https://latex.codecogs.com/svg.latex?\Large&space;ln(N) = 12.666909387   "/>&nbsp;&nbsp;
  donc la condition n'est pas verifié<br />
-Donc un réseau aléatoire avec cette taille sera aléatoire à partir d'un degré 
moyen superieur à <img src="https://latex.codecogs.com/svg.latex?\Large&space;k > 12.666909387  "/>   <br />
----
### 4-La distribution des degrés
 -Il faut créer un fichier contenant les degrés et leurs distributions, en executant
  avec gnuplot on aura ces 2 resultats:  
 
 
 | distribution linéare            |    |
 :--------------------------:|:-------------------------:
 ![](src/main/resources/dl.png)  |  

 <br /><br />
 
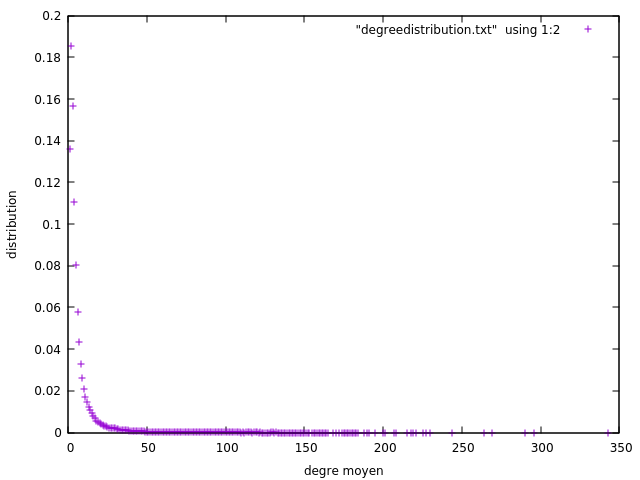 | distribution log log            |    |
  :--------------------------:|:-------------------------:
  ![](src/main/resources/dlog.png) |
 
 


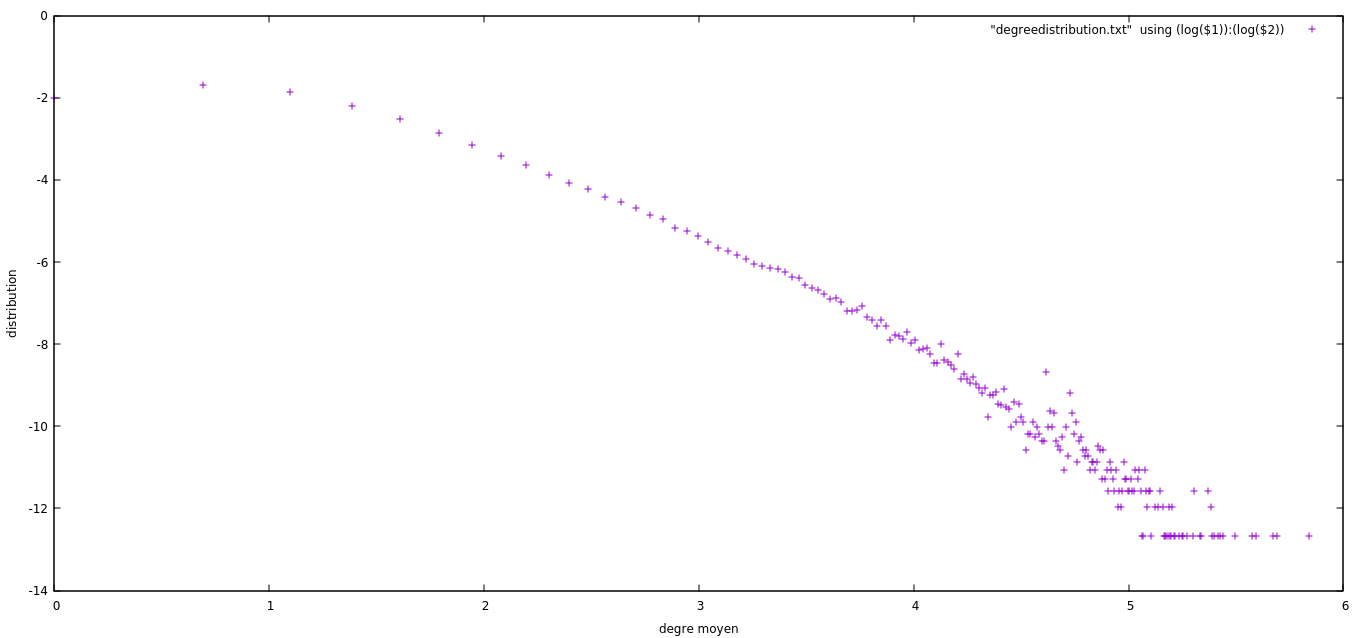En traçant la distribution de degrés en échelle log-log on observe une ligne droite 
pendant plusieurs ordres de grandeur. Cela nous indique une loi de puissance : 
<img src="https://latex.codecogs.com/svg.latex?\Large&space;P_k=CK^\delta"/>

-tracer la distribution et estimer l'exposant de la loi de puissance:
<br /><br />

 | distribution log log            |    |   
  :--------------------------:|:-------------------------:
  ![](src/main/resources/dd_dblp.png) |

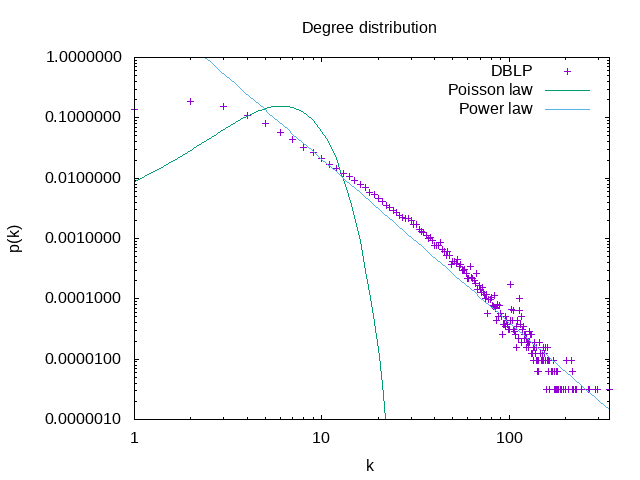On a γ=2.7±0.04
----
### 5-La distance moyenne dans le réseau