# Mesures de réseaux d'interaction
Nous allons analyser un réseau de collaboration scientifique en informatique. Le réseau est extrait de DBLP et disponible sur [SNAP](https://snap.stanford.edu/data/com-DBLP.html).
GraphStream permet de mesurer de nombreuses caractéristiques d'un réseau. La plupart de ces mesures sont implantées comme des méthodes statiques dans la classe [`Toolkit`](https://data.graphstream-project.org/api/gs-algo/current/org/graphstream/algorithm/Toolkit.html). Elles vous seront très utiles par la suite.
1. Commencez par télécharger les données et les lire avec GraphStream. GraphStream sait lire ce format. Voir [`FileSourceEdge`](https://data.graphstream-project.org/api/gs-core/current/org/graphstream/stream/file/FileSourceEdge.html) et ce [tutoriel](http://graphstream-project.org/doc/Tutorials/Reading-files-using-FileSource/). Vous pouvez essayer de visualiser le graphe mais pour cette taille ça sera très lent et très peu parlant.
**DONE**
2. Prenez quelques mesures de base: nombre de nœuds et de liens, degré moyen, coefficient de clustering. Quel sera le coefficient de clustering pour un réseau aléatoire de la même taille et du même degré moyen ?
- Nombre de noeuds : **317080**
- Nombre de liens : **1049866**
- Degré moyen : **~6.622**
- Coefficient de Clustering : **~0.6324**
**Réseau aléatoire**
- Coefficient de Clustering : Degres moyen de g/Nombre noeud dans g = **2.0884599814397534E-5** il est différent car il s'agit d'un réseau aléatoire.
3. Le réseau est-il connexe ? Un réseau aléatoire de la même taille et degré moyen sera-t-il connexe ? À partir de quel degré moyen un réseau aléatoire avec cette taille devient connexe ?
- Le réseau est bien connexe
- Le réseau aléatoire n'est pas connexe si l'on garde le même degrès et nombres de noeuds, car le degrès moyen n'est pas supérieur à log(Nombre de noeuds).
- On a ln(N) = 12,67 et Degres moyen = 6.22. Il faut donc que le Degres Moyen > a ln(N) soit environ à partir de 12,68.
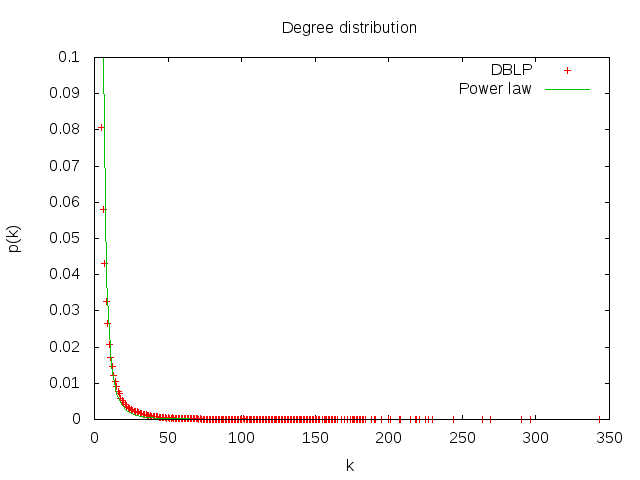
4. Calculez la distribution des degrés et tracez-la avec `gnuplot` (ou avec votre outil préféré) d'abord en échelle linéaire, ensuite en échelle log-log. Est-ce qu'on observe une ligne droite en log-log ? Que cela nous indique ? Tracez la distribution de Poisson avec la même moyenne pour comparaison. Utilisez la commande `fit` de `gnuplot` pour trouver les coefficients de la loi de puissance et tracez-la.
**Graphique en Linéaire**
**Graphique Log-Log**
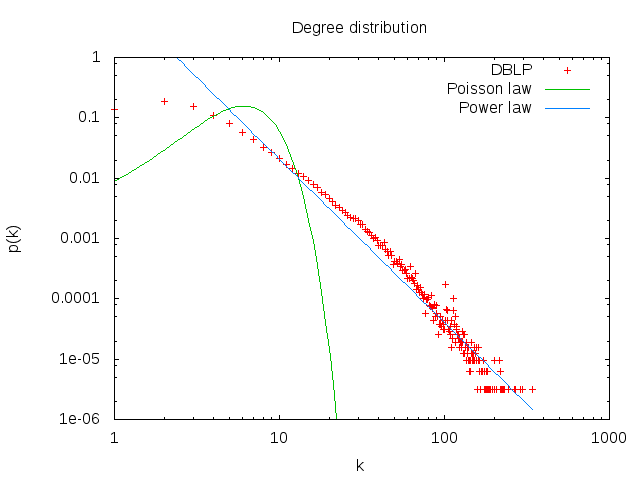
- On observe une ligne droite en log-log ce qui signifie qu'on a une loi de puissance :
```math
p_k = C k^{-\gamma}
```
5. Maintenant on va calculer la distance moyenne dans le réseau. Le calcul des plus courts chemins entre toutes les paires de nœuds prendra plusieurs heures pour cette taille de réseau. C'est pourquoi on va estimer la distance moyenne par échantillonnage en faisant un parcours en largeur à partir de 1000 sommets choisis au hasard. L'hypothèse des six degrés de séparation se confirme-t-elle ? Est-ce qu'il s'agit d'un réseau petit monde ? Quelle sera la distance moyenne dans un réseau aléatoire avec les mêmes caractéristiques ? Tracez également la *distribution* des distances. Formulez une hypothèse sur la loi de cette distribution.
L'hypothese se confirme parce qu'on obtient une distance moyenne de 6,83 qui est supérieur à 6.
Il s'agit donc bien d'un réseau petit monde car on a une connection entre 6 personnes environ.
La moyenne dans un réseau aléatoire de même caractéristique et de 6.701. ln(N)/ln(k)
**Graphique linéaire de la distribution des longueurs**
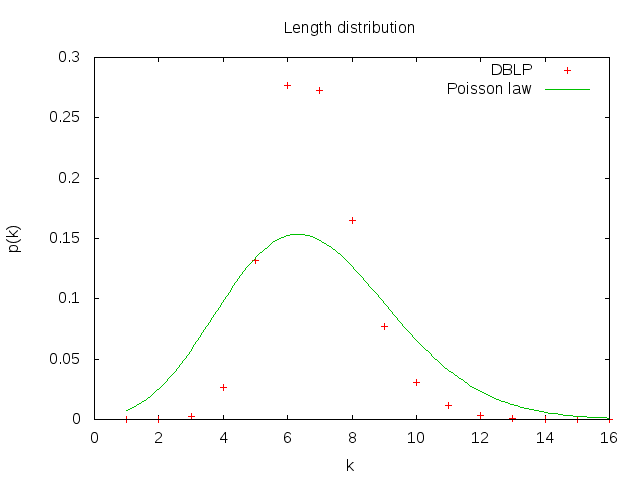
Le graphique ressemble à une loi de poisson avec un pic situé au même endroit sur le graphe.
6. Utilisez les générateurs de GraphStream pour générer un réseau aléatoire et un réseau avec la méthode d'attachement préférentiel (Barabasi-Albert) qui ont la même taille et le même degré moyen. Refaites les mesures des questions précédentes pour ces deux réseaux. Les résultats expérimentaux correspondent-ils aux prédictions théoriques ? Comparez avec le réseau de collaboration. Que peut-on conclure ?
**Réseau aléatoire**
Nombre de noeuds : 317087
Nombre de liens : 1051246
Degre moyen : 6.6306471824646
Coefficient de clustering : 2.298692400722293E-5
le graphe est connexe : false
somme = 3422209 | nb = 499500
Longeur moyenne = 6.851269269269269
Comme dit dans la question 2 on a :
Nombre de noeud : Théorie : 317080 / Pratique : 317087
Nombre de lien : Théorie : 1049866 / Pratique : 1051246
Degres Clustering : Théorie : 2.0884599814397534E-5 / Pratique : 2.298692400722293E-5
On remarque que les données sont similaires entre la partie théorique et la partie pratique por un réseau aléatoire
**Graphe Barabasi-Albert**
Comme dit dans la question 2 on a :
Nombre de noeud : Théorie : 317080 / Pratique : 317082
Nombre de lien : Théorie : 1049866 / Pratique : 1111512
Degres Clustering : Théorie : 2.0884599814397534E-5 / Pratique : 4.04E-4
On remarque que les données sont différentes entre la partie théorique et la partie pratique pour un graphe de Barabasi-Albert
# Propagation dans des réseaux
Nos collaborateurs scientifiques communiquent souvent par mail. Malheureusement pour eux, les pièces jointes de ces mails contiennent parfois des virus informatiques. On va étudier la propagation d'un virus avec les hypothèses suivantes :
- Un individu envoie en moyenne un mail par semaine à chacun de ses collaborateurs.
- Un individu met à jour son anti-virus en moyenne deux fois par mois. Cela nettoie son système mais ne le protège pas de nouvelles infections car le virus mute.
- L'épidémie commence avec un individu infecté (patient zéro).
1. Quel est le taux de propagation du virus ? Quel est le seuil épidémique du réseau ? Comparez avec le seuil théorique d'un réseau aléatoire du même degré moyen.
- Taux de propagation : En moyenne 1 mail par semaine soit β = 1/7
et mise a jour de l'ordinateur 2 fois par moi soit µ = 1/14.
On a donc β/µ = 2.0
- Le seuil épidémique du réseau est :
Notre réseau suit une loi de puissance comme vu lors du dernier TP avec le graohique sur la distribution des degrees.
On utilise la donc la formule (k)/(k)^2 pour calculer le seuil épidémique λc du réseau
λc = 0.04598472436222584 on remarque que λ > λc donc on peut conclure que la maladie persiste.
- Le seuil épidémique d'un réseau aléatoire
On applique théoriquement la forume 1/((k)+1) on option λc = 0.13119762993051035
- On remarque que le seuil épidémique et nettement plus faible dans un réseau sans échelle que dans un réseau aléatoire.
2.