### DM -Théorie des graphes - M1 - IWOCS
---
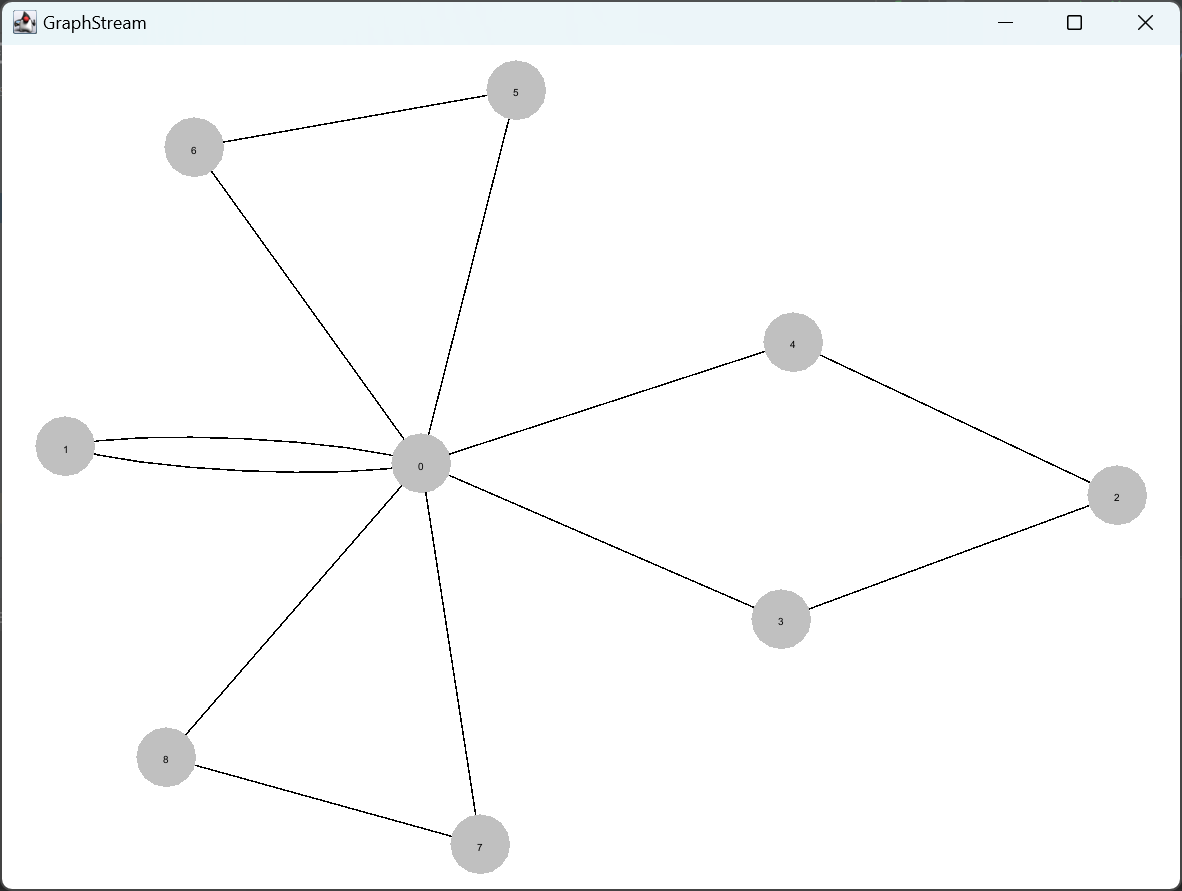
1. __Application de Algorithme de Clarke and Wright__
- table des quantité requise par les sommets du graphe G
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|------|-----|-----|-----|-----|-----|----|-----|-----|
| k(s) | 7 | 2 | 1 | 4 | 5 | 1 | 3 | 4 |
- table des temps d'acheminement
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|
|0 | 0 | 22 | 28 | 20 | 10 | 19 | 19 | 36 | 37 |
|1 | 22 | 0 | 30 | 36 | 17 | 7 | 14 | 60 | 60 |
|2 | 28 | 30 | 0 | 20 | 18 | 34 | 39 | 60 | 60 |
|3 | 20 | 36 | 20 | 0 | 18 | 36 | 38 | 50 | 50 |
|4 | 10 | 17 | 18 | 18 | 0 | 18 | 22 | 50 | 50 |
|5 | 19 | 7 | 34 | 36 | 18 | 0 | 6 | 50 | 50 |
|6 | 19 | 14 | 39 | 38 | 22 | 6 | 0 | 50 | 50 |
|7 | 36 | 60 | 60 | 50 | 50 | 50 | 50 | 0 | 7 |
|8 | 37 | 60 | 60 | 50 | 50 | 50 | 50 | 7 | 0 |
- table des sauvegardes
| i,j | 1, 2 | 1, 3 | 1, 4 | 1, 5 | 1, 6 | 1, 7 | 1, 8 | 2, 3 | 2, 4 | 2, 5 | 2, 6 | 2, 7 | 2, 8 | 3, 4 | 3, 5 | 3, 6 | 3, 7 | 3, 8 | 4, 5 | 4, 6 | 4, 7 | 4, 8 | 5, 6 | 5, 7 | 5, 8 | 6, 7 | 6, 8 | 7, 8 |
|--------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|
| s(i,j) | 20 | 6 | 15 | 34 | 27 | -2 | -1 | 28 | 20 | 13 | 8 | 4 | 5 | 12 | 3 | 1 | 6 | 7 | 11 | 7 | -4 | -3 | 32 | 5 | 6 | 5 | 6 | 66 |
- liste `S` decroissante des sauvegardes avec leurs indices :
| i,j | 7, 8 | 1, 5 | 5, 6 | 2, 3 | 1, 6 | 1, 2 | 2, 4 | 1, 4 | 2, 5 | 3, 4 | 4, 5 | 2, 6 | 3, 8 | 4, 6 | 1, 3 | 3, 7 | 5, 8 | 6, 8 | 2, 8 | 5, 7 | 6, 7 | 2, 7 | 3, 5 | 3, 6 | 1, 8 | 1, 7 | 4, 8 | 4, 7 |
|--------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|------|
| s(i,j) | 66 | 34 | 32 | 28 | 27 | 20 | 20 | 15 | 13 | 12 | 11 | 8 | 7 | 7 | 6 | 6 | 6 | 6 | 5 | 5 | 5 | 4 | 3 | 1 | -1 | -2 | -3 | -4 |
- Parcourrir `S` en applicant l'instruction d'ajout et de suppression de route
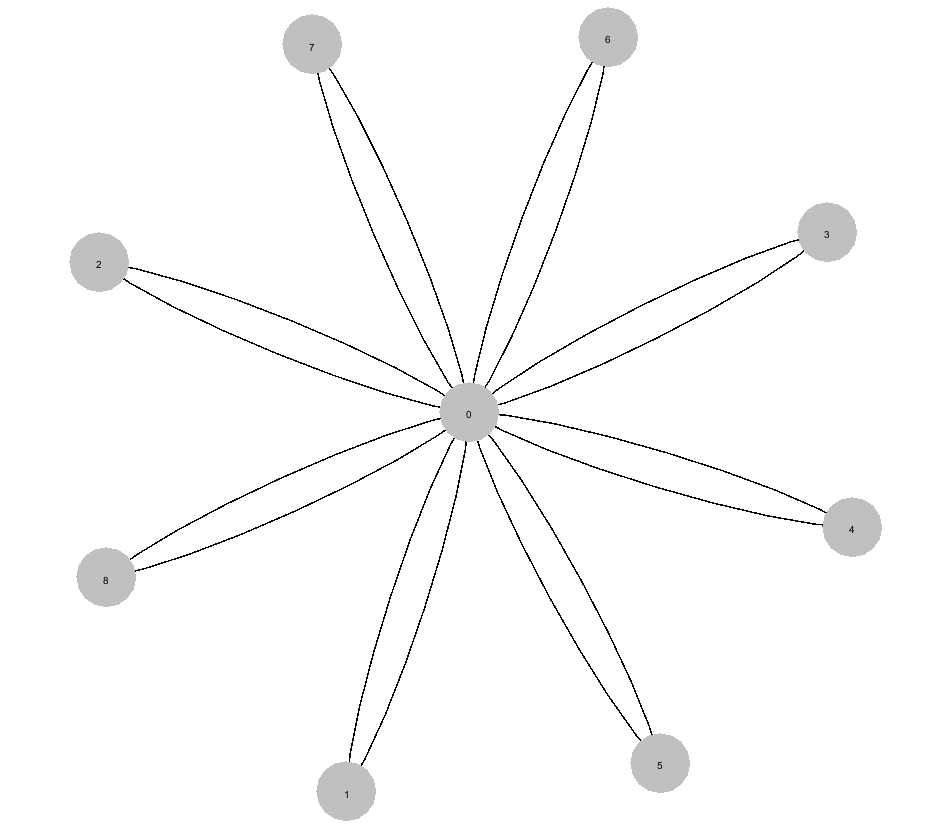
> `k7 + K8 = 3 + 4 = 7 < 10` on connect donc 7 et 8
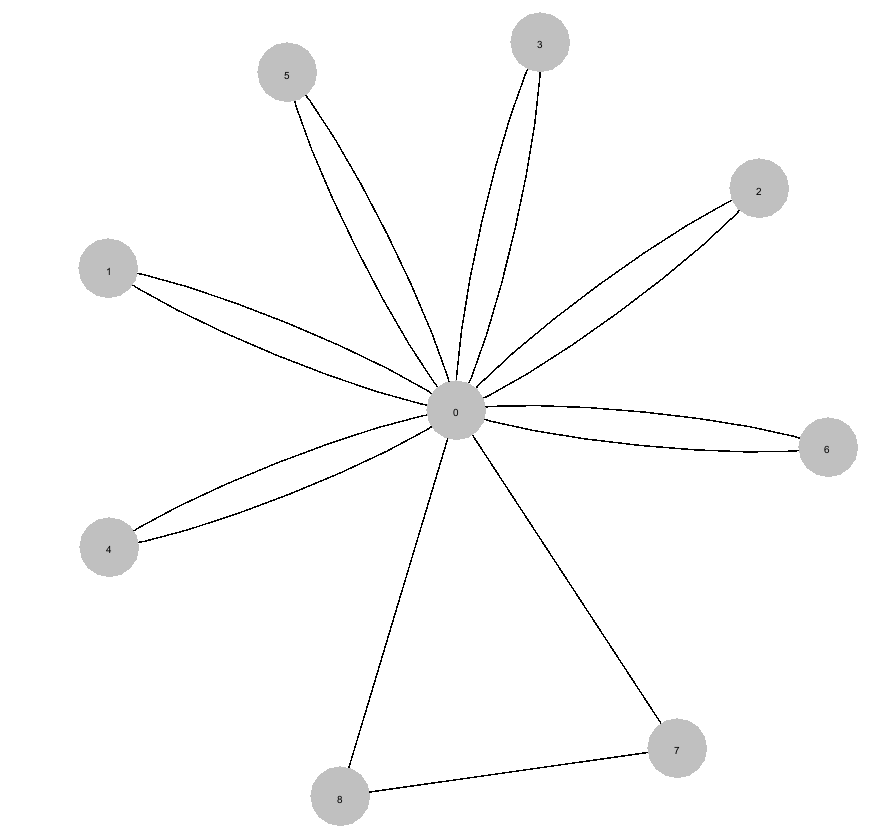
> - `k1 + K5 = 7 + 5 = 12 > 10` on passe
> - `k5 + K6 = 5 + 1 = 6 < 10` on connect donc 5 et 6
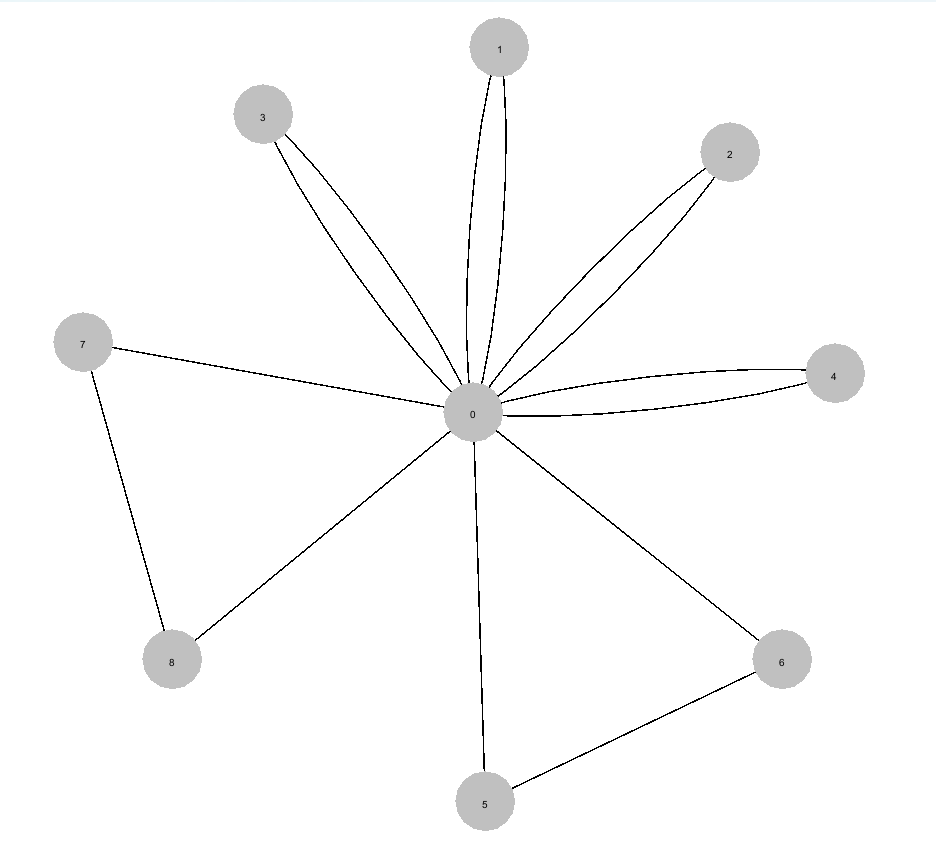
> `k2 + K3 = 2 + 1 = 3 < 10` on connect donc 2 et 1 #K2_3
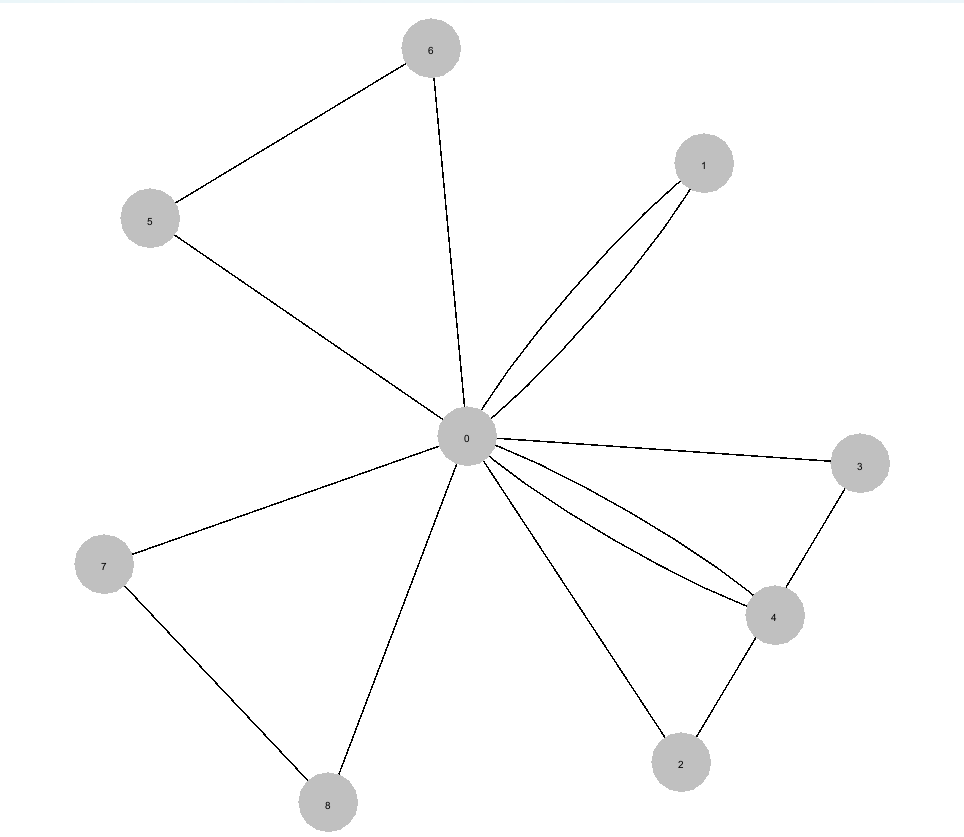
> `k1 + K6_5 = 7 + 6 = 13 > 10` on connect passe
> `k1 + K2_3 = 7 + 3 = 10` on passe
> `k2_3 + K4 = 3 + 4 = 7 < 10` on connect donc 2 et 4
> - `k1 + K4_2_3 = 7 + 7 = 14 > 10` on passe
> - `(2, 5)` on a pas de (0, 2) on passe
> - `(3, 4)` deja sur la même route
> - `k4 + K5 = 7 + 5 = 12 < 10` on passe
> - `(2, 6)` on a pas de (0, 2) on passe
> - `k3 + K8 = 7 + 7 = 14 > 10` on connect donc 7 et 8
> - `k4 + k6 = 7 + 6` on passe
> - `k1 + k3 = 7+ 7` on passe
> - `k3 + K7 = 7 + 7` on passe
> - `k5 + K8 = 6 + 7` on passe
> - `k6 + K8 = 6 + 7` on passe
> - `(2, 8)` on passe car pas de (0, 2)
> - `k5 + K7 = 6 + 7` on passe
> - `k6 + K7 = 6 + 7` on passe
> - `(2, 7)` on passe car pas de (0, 2)
> - `k3 + K5 = 7 + 6` on passe
> - `k3 + K6 = 7 + 6` on passe
> - les capacités restantes etant inferieure à `0` on sort donc de la boucle
2. __Exemple où l’heuristique de Clarke and Wright ne donne pas la solution optimale__
3. __Complexité de l'algorithme de Clarke and Wright__
| instruction | nombres d'operation | complexité |
|:------------------------------|:-------------------:|-----------:|
| calclul des S(i,j) | n(n-1)/2 | θ(n²) |
| trier S `(tri par insertion)` | n(n-1)/2 | θ(n²) |
| suppresion de route | 1 | θ(1) |
| ajout de route | 1 | θ(1) |
| teste E(0,i) | 1 | θ(1) |
| teste E(0,j) | 1 | θ(1) |
| Ki + kj | 1 | θ(1) |
| teste Ki_j> c | 1 | θ(1) |
| teste S(i,j)> 0 | 1 | θ(1) |
| iteration sur S | n² + 7 | θ(n²) |
la complexité de cet algorithme est donc de θ(n²)